【理論】平成27年 問17|三相交流回路における三相電力とコンデンサ容量の計算問題
図のような \( \mathrm{V} \) 結線電源と三相平衡負荷とからなる平衡三相回路において,\( R = 5 \) [Ω],\( L = 16 \) [mH] である。
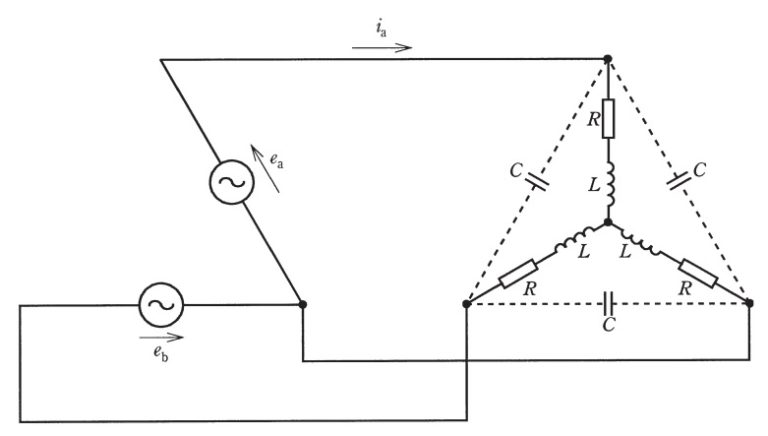
また,電源の線間電圧 \( e_{\mathrm{a}} \) [V] は,時刻 \( t \) [s] において,\( e_{\mathrm{a}} = 100\sqrt{6} \sin \left( 100\pi t \right) \) [V] と表され,線間電圧 \( e_{\mathrm{b}} \) [V] は \( e_{\mathrm{a}} \) [V] に対して振幅が等しく,位相が \( 120^\circ \) 遅れている。
ただし,電源の内部インピーダンスは零である。
このとき,次の (a) 及び (b) の問に答えよ。
(a) 図の点線で示された配線を切断し,3 個のコンデンサを三相回路から切り離したとき,三相電力 \( P \) の値 [kW] として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
(b) 点線部を接続することによって同じ特性の 3 個のコンデンサを接続したところ,\( i_{\mathrm{a}} \) の波形は \( e_{\mathrm{a}} \) の波形に対して位相が \( 30^\circ \) 遅れていた。
このときのコンデンサ \( C \) の静電容量の値 [F] として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
合格への方程式
リアクトルとコンデンサのリアクタンス
リアクトル(インダクタ)とコンデンサは、交流回路において電流の流れに対して抵抗のような働きをします。この抵抗のような性質を「リアクタンス」と呼びます。
リアクタンスは周波数に依存する値で、直流回路では異なる振る舞いをします。
インダクタンスが \(L \ \mathrm{[H]}\) のリアクトルと静電容量 \(C \ \mathrm{[F]}\) のコンデンサの各リアクタンス \(X_{\mathrm{L}} \ [\Omega]\) と \(X_{\mathrm{C}} \ [\Omega]\) の大きさは、角周波数を \(\omega \ \mathrm{[rad/s]}\) とすると、次の式で表されます:
\[ \begin{aligned} X_{\mathrm{L}} &= \mathrm{j}\omega L \\[10pt] X_{\mathrm{C}} &= \frac{1}{\mathrm{j}\omega C} \\[10pt] \end{aligned} \]
ここで、j は虚数単位 \(j = \sqrt{-1}\) を表します。リアクタンスが虚数で表されるのは、抵抗(レジスタンス)とは異なり、電圧と電流の間に位相差が生じるためです。
リアクトルのリアクタンス \(X_{\mathrm{L}}\) は周波数に比例して大きくなりますが、コンデンサのリアクタンス \(X_{\mathrm{C}}\) は周波数に反比例して小さくなります。
Δ-Y変換
Δ(デルタ)接続をY(スター)接続に変換する方法です。この変換を使うと、複雑な回路の解析が簡単になることがあります。
図1:Δ接続とY接続の対応関係
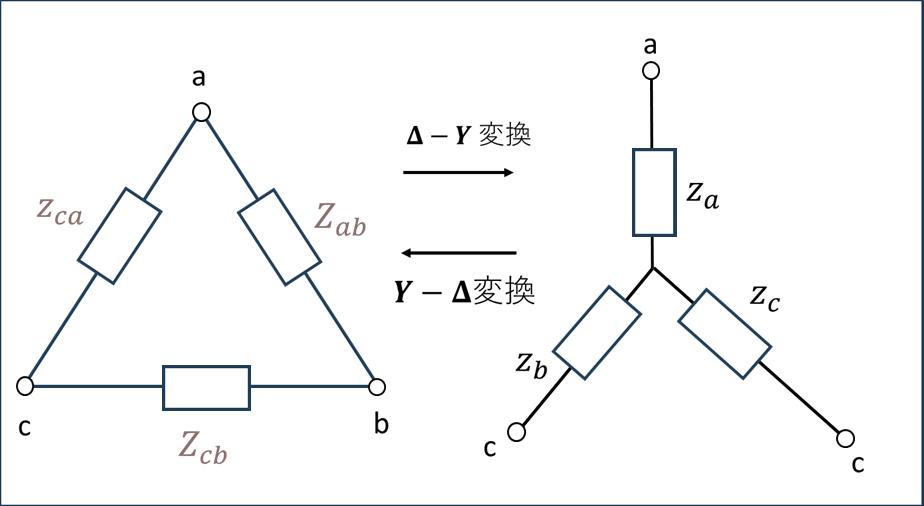
図1において、Δ接続のインピーダンス \(Z_{\mathrm{ab}}\)、\(Z_{\mathrm{bc}}\)、\(Z_{\mathrm{ca}}\) からY接続のインピーダンス \(Z_{\mathrm{a}}\)、\(Z_{\mathrm{b}}\)、\(Z_{\mathrm{c}}\) を求める変換式は以下の通りです:
\[ \begin{aligned} Z_{\mathrm{a}} &= \frac{Z_{\mathrm{ab}}Z_{\mathrm{ca}}}{Z_{\mathrm{ab}}+Z_{\mathrm{bc}}+Z_{\mathrm{ca}}} \\[10pt] Z_{\mathrm{b}} &= \frac{Z_{\mathrm{bc}}Z_{\mathrm{ab}}}{Z_{\mathrm{ab}}+Z_{\mathrm{bc}}+Z_{\mathrm{ca}}} \\[10pt] Z_{\mathrm{c}} &= \frac{Z_{\mathrm{ca}}Z_{\mathrm{bc}}}{Z_{\mathrm{ab}}+Z_{\mathrm{bc}}+Z_{\mathrm{ca}}} \\[10pt] \end{aligned} \]
各式の分母はすべて同じで、分子は変換したいY接続の端子に接続されているΔ接続の2つのインピーダンスの積になっています。
Y-Δ変換
Y(スター)接続をΔ(デルタ)接続に変換する方法です。Δ-Y変換の逆変換になります。
図1:Y接続とΔ接続の対応関係

図1において、Y接続のインピーダンス \(Z_{\mathrm{a}}\)、\(Z_{\mathrm{b}}\)、\(Z_{\mathrm{c}}\) からΔ接続のインピーダンス \(Z_{\mathrm{ab}}\)、\(Z_{\mathrm{bc}}\)、\(Z_{\mathrm{ca}}\) を求める変換式は以下の通りです:
\[ \begin{aligned} Z_{\mathrm{ab}} &= \frac{Z_{\mathrm{a}}Z_{\mathrm{b}}+Z_{\mathrm{b}}Z_{\mathrm{c}}+Z_{\mathrm{c}}Z_{\mathrm{a}}}{Z_{\mathrm{c}}} \\[10pt] Z_{\mathrm{bc}} &= \frac{Z_{\mathrm{a}}Z_{\mathrm{b}}+Z_{\mathrm{b}}Z_{\mathrm{c}}+Z_{\mathrm{c}}Z_{\mathrm{a}}}{Z_{\mathrm{a}}} \\[10pt] Z_{\mathrm{ca}} &= \frac{Z_{\mathrm{a}}Z_{\mathrm{b}}+Z_{\mathrm{b}}Z_{\mathrm{c}}+Z_{\mathrm{c}}Z_{\mathrm{a}}}{Z_{\mathrm{b}}} \\[10pt] \end{aligned} \]
各式の分子はすべて同じで \(Z_{\mathrm{a}}Z_{\mathrm{b}}+Z_{\mathrm{b}}Z_{\mathrm{c}}+Z_{\mathrm{c}}Z_{\mathrm{a}}\) となります。分母は、求めたいΔ接続の辺に対応しない(向かい合う)Y接続の端子のインピーダンスです。
平衡三相回路
平衡三相回路とは、3つの相のインピーダンスがすべて等しい回路のことです。このような回路では、Δ-Y変換とY-Δ変換の式が簡単になります。
平衡三相回路では、以下の関係が成り立ちます:
\[ Z_{\mathrm{ab}} = Z_{\mathrm{bc}} = Z_{\mathrm{ca}} = 3Z_{\mathrm{a}} = 3Z_{\mathrm{b}} = 3Z_{\mathrm{c}} \]
つまり、平衡三相回路においては、Δ接続のインピーダンスはY接続のインピーダンスの3倍になります。この関係は、電力系統や三相モーターなどの解析で役立ちます。
平衡三相回路の場合、各相の電圧や電流の大きさは等しく、位相が120度ずつずれているという特徴があります。
🔍 ワンポイントアドバイス: リアクタンスには周波数依存性があります。インダクタは周波数が高くなるほどリアクタンスが大きくなり、コンデンサは逆に小さくなります。また、Δ-Y変換は複雑な回路の簡略化や解析に役立ちますが、変換前後でインピーダンスの値が変わることに注意しましょう。
まずは(a)問題から取り組んでいくで。問題では三相交流電源と三相平衡負荷の回路が出てきてるな。三相交流電源の線間電圧と相電圧の関係、わかるかな?
はい、先生!三相交流電源において、線間電圧と相電圧の関係は以下のようになります:
・Y結線(スター結線)の場合:線間電圧 = √3 × 相電圧
・Δ結線(デルタ結線)の場合:線間電圧 = 相電圧
問題では電源電圧の実効値Eaが100√3 [V]と与えられているので、これを相電圧に変換する必要があります。
ええやん!じゃあ実効値Eaから相電圧の実効値Eapを求めるで。まず電源電圧eaがどないなってるか確認してみよか?
問題文より、電源電圧eaの実効値Eaは100√3 [V]であることがわかります。この値は次のような計算で求められています:
\[ \begin{aligned} E_a &= \frac{100\sqrt{6}}{\sqrt{2}} \\[10pt] &= 100\sqrt{3} \ \mathrm{[V]} \end{aligned} \]これは線間電圧の実効値だと考えられます。Y結線の場合、相電圧の実効値Eapは線間電圧を√3で割った値になります:
\[ \begin{aligned} E_{ap} &= \frac{100\sqrt{3}}{\sqrt{3}} \\[10pt] &= 100 \ \mathrm{[V]} \end{aligned} \]よって、相電圧の実効値Eapは100 [V]です。
ようわかっとるな!さて、この回路は三相平衡負荷やから、一相分の等価回路で計算できるんや。図1の等価回路はどんなになるやろ?
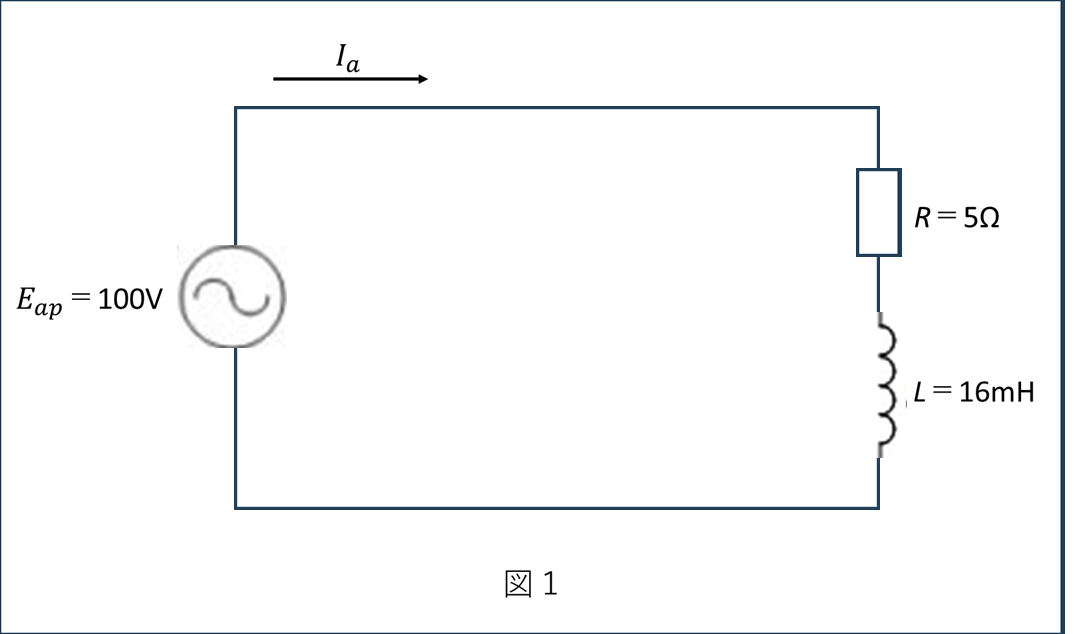
三相平衡負荷の場合、各相は同じ条件で動作するため、一相分だけを取り出して計算できます。図2の等価回路は、一相あたりの相電圧源Eapと、それに接続された直列のR-L回路(抵抗RとコイルL)で構成されます。
具体的には:
・電源:相電圧Eap = 100 [V]
・抵抗:R = 5 [Ω]
・インダクタンス:L = 16×10⁻³ [H]
・角周波数:ω = 100π [rad/s]
そのとおりや!じゃあこの回路に流れる電流Iaを計算してみよか。インピーダンスの考え方を使うんやで。
一相あたりの電流Iaを計算するために、まず回路のインピーダンスを求めます。
抵抗RのインピーダンスはR = 5 [Ω]
コイルLのインピーダンスはjωL = j × 100π × 16×10⁻³ = j5.02654 [Ω]
合成インピーダンスZは:
\[ \begin{aligned} Z &= R + j\omega L \\[10pt] &= 5 + j(100\pi \times 16 \times 10^{-3}) \\[10pt] &= 5 + j5.02654 \ \mathrm{[\Omega]} \end{aligned} \]インピーダンスの大きさ|Z|は:
\[ \begin{aligned} |Z| &= \sqrt{R^2 + (\omega L)^2} \\[10pt] &= \sqrt{5^2 + (100\pi \times 16 \times 10^{-3})^2} \\[10pt] &= \sqrt{25 + 25.26605} \\[10pt] &= \sqrt{50.26605} \\[10pt] &\approx 7.0898 \ \mathrm{[\Omega]} \end{aligned} \]よって、電流の大きさIaは:
\[ \begin{aligned} I_a &= \frac{E_{ap}}{|Z|} \\[10pt] &= \frac{100}{7.0898} \\[10pt] &= 14.108 \ \mathrm{[A]} \end{aligned} \]ナイス計算や!じゃあ最後に三相電力Pを求めるで。三相平衡負荷での電力計算、覚えてるか?
三相平衡負荷での有効電力Pは、一相あたりの有効電力に3を掛けることで求められます。一相あたりの有効電力は、抵抗Rでの消費電力I²Rです。
\[ \begin{aligned} P &= 3RI_a^2 \\[10pt] &= 3 \times 5 \times 14.108^2 \\[10pt] &= 15 \times 199.04 \\[10pt] &= 2985.6 \ \mathrm{[W]} \\[10pt] &\approx 3 \ \mathrm{[kW]} \end{aligned} \]したがって、三相電力Pは約3 [kW]となり、選択肢(2)が正解です。
よっしゃ!(a)問題はばっちりや。次に(b)問題に移るで。力率改善のためのコンデンサの容量を求める問題やな。まずこの問題で大事なのは、力率1(遅れも進みもない)にするってことやけど、それはどういう条件になるか考えてみ?
力率1(力率が100%)にするということは、回路の電流と電圧が同相(位相差がゼロ)になるように調整することです。
現在の回路では、コイルLがあるため、電流は電圧に対して遅れています。この遅れを打ち消すために、適切な容量のコンデンサCを並列に接続します。
力率1を実現するためには、回路の合成インピーダンスの虚数部(リアクタンス成分)がゼロになるように、コンデンサの容量Cを選ぶ必要があります。つまり、コイルの誘導性リアクタンスjωLをコンデンサの容量性リアクタンス-j/(ωC)で相殺します。
そのとおりや!問題では、コンデンサがΔ結線で接続されとるけど、計算しやすいようにY結線に変換するんやな。Δ-Y変換の公式、覚えてるか?
はい、Δ結線からY結線への変換(Δ-Y変換)では、インピーダンス(またはアドミタンス)の関係は以下のようになります:
Δ結線のインピーダンスをZΔ、変換後のY結線のインピーダンスをZYとすると:
\( Z_Y = \frac{Z_{\Delta}}{3} \)または、アドミタンス(インピーダンスの逆数)を使うと:
\( Y_Y = 3Y_{\Delta} \)コンデンサの場合、キャパシタンスCに置き換えると:
\[ \begin{aligned} \frac{1}{\omega C'} &= \frac{1}{3\omega C} \\[10pt] C' &= 3C \end{aligned} \]つまり、Δ結線のコンデンサ容量CをY結線に変換すると、Y結線での等価容量はC' = 3Cとなります。
ナイスや!じゃあY結線に変換した後の一相分の等価回路はどうなる?図2の回路を説明してみてくれるか?
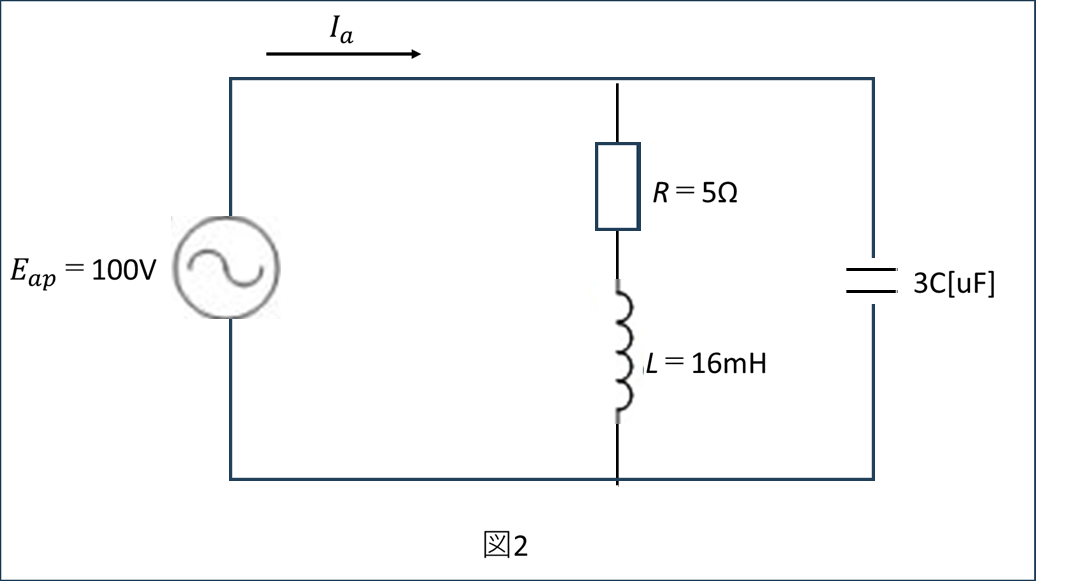
Y結線に変換した後の一相分の等価回路(図3)は、以下のような構成になります:
1. 相電圧源Eap = 100 [V]
2. 負荷側には直列接続された抵抗RとコイルL(R = 5 [Ω]、L = 16×10⁻³ [H])
3. 上記の直列R-L回路と並列に接続されたコンデンサC'(= 3C)
この回路では、電源から見た合成インピーダンスZは、R-L直列回路とコンデンサC'の並列接続になります。
さすがやな!じゃあこの回路の合成インピーダンスを計算していくで。並列回路の合成インピーダンスの公式を使って計算するんやけど、どう計算する?
並列回路の合成インピーダンスは、各インピーダンスの逆数(アドミタンス)の和の逆数として計算できます。
R-L直列回路のインピーダンス:Z₁ = R + jωL
コンデンサのインピーダンス:Z₂ = 1/(jωC') = 1/(j3ωC)
合成インピーダンスZは:
\[ \begin{aligned} Z &= \frac{Z_1 \cdot Z_2}{Z_1 + Z_2} \\[10pt] &= \frac{(R + j\omega L) \cdot \frac{1}{j3\omega C}}{(R + j\omega L) + \frac{1}{j3\omega C}} \\[10pt] &= \frac{(R + j\omega L)}{j3\omega C \cdot (R + j\omega L) + 1} \\[10pt] &= \frac{(R + j\omega L)}{j3\omega RC - 3\omega^2 LC + 1} \\[10pt] &= \frac{(R + j\omega L)}{1 - 3\omega^2 LC + j3\omega RC} \end{aligned} \]完璧や!これを使って電流Iaを計算するんやけど、どうやって計算していくか説明してみてくれるか?
電流Iaは、相電圧Eapを合成インピーダンスZで割ることで計算できます:
\[ \begin{aligned} I_a &= \frac{E_{ap}}{Z} \\ &= E_{ap} \cdot \frac{1 - 3\omega^2 LC + j3\omega RC}{R + j\omega L} \end{aligned} \]この式をさらに計算するために、分子と分母を実数部と虚数部に分けます。まず、分母を有理化(実数と虚数に分離)するために、分子・分母に分母の共役複素数をかけます:
\[ \begin{aligned} I_a &= E_{ap} \cdot \frac{(1 - 3\omega^2 LC + j3\omega RC)(R - j\omega L)}{(R + j\omega L)(R - j\omega L)} \\[10pt] &= E_{ap} \cdot \frac{(1 - 3\omega^2 LC + j3\omega RC)(R - j\omega L)}{R^2 + (\omega L)^2} \end{aligned} \]分子の括弧を展開します:
\[ \begin{aligned} &(1 - 3\omega^2 LC + j3\omega RC)(R - j\omega L) \\[10pt] &= R(1 - 3\omega^2 LC) - j\omega L(1 - 3\omega^2 LC) + j3\omega RC \cdot R - j^2 3\omega RC \cdot \omega L \\[10pt] &= R(1 - 3\omega^2 LC) - j\omega L(1 - 3\omega^2 LC) + j3\omega R^2C + 3\omega^2 RLC \\[10pt] &= R(1 - 3\omega^2 LC) + 3\omega^2 RLC - j\omega L(1 - 3\omega^2 LC) + j3\omega R^2C \\[10pt] &= R - 3\omega^2 RLC + 3\omega^2 RLC - j\omega L + j3\omega^2 L^2C + j3\omega R^2C \\[10pt] &= R + j[3\omega R^2C - \omega L(1 - 3\omega^2 LC)] \end{aligned} \]したがって、電流Iaは:
\[ \begin{aligned} I_a &= E_{ap} \cdot \frac{R + j[3\omega R^2C - \omega L(1 - 3\omega^2 LC)]}{R^2 + (\omega L)^2} \end{aligned} \]とてもよく理解できとるな!さて、力率1にするためには電流と電圧が同相、つまり電流の虚数部がゼロにならなあかんのやけど、その条件はどうなる?
力率1にするためには、電流Iaの虚数部がゼロになる必要があります。先ほど計算した電流式の虚数部を見ると:
\[ \begin{aligned} 3\omega R^2C - \omega L(1 - 3\omega^2 LC) = 0 \end{aligned} \]この方程式を解いて、コンデンサの容量Cを求めます。
\[ \begin{aligned} 3\omega R^2C - \omega L(1 - 3\omega^2 LC) &= 0 \\[10pt] 3\omega R^2C - \omega L + 3\omega^3 L^2C &= 0 \\[10pt] 3\omega R^2C + 3\omega^3 L^2C &= \omega L \\[10pt] 3\omega C(R^2 + \omega^2 L^2) &= \omega L \\[10pt] 3C(R^2 + \omega^2 L^2) &= L \\ C &= \frac{L}{3(R^2 + \omega^2 L^2)} \end{aligned} \]素晴らしい!じゃあ最後に具体的な数値を代入してCの値を計算しよか。
コンデンサの容量Cを計算するために、具体的な数値を代入します:
・抵抗:R = 5 [Ω]
・インダクタンス:L = 16×10⁻³ [H]
・角周波数:ω = 100π [rad/s]
\[ \begin{aligned} C &= \frac{L}{3(R^2 + \omega^2 L^2)} \\[10pt] &= \frac{16 \times 10^{-3}}{3 \times [5^2 + (100\pi)^2 \times (16 \times 10^{-3})^2]} \\[10pt] &= \frac{16 \times 10^{-3}}{3 \times [25 + (100\pi)^2 \times (16 \times 10^{-3})^2]} \\[10pt] &= \frac{16 \times 10^{-3}}{3 \times [25 + 25.26605]} \\[10pt] &= \frac{16 \times 10^{-3}}{3 \times 50.26605} \\[10pt] &= \frac{16 \times 10^{-3}}{150.798} \\[10pt] &\approx 0.1061 \times 10^{-3} \ \mathrm{[F]} \\[10pt] &\approx 1.1 \times 10^{-4} \ \mathrm{[F]} \end{aligned} \]したがって、力率1を実現するために必要なΔ結線のコンデンサ容量Cは約1.1×10⁻⁴ [F]となり、選択肢(2)が正解です。
ほんま頑張ったな!最後にこの問題の重要なポイントをまとめておこか?
はい、先生!この問題の重要なポイントをまとめます:
1. 三相交流回路では、三相平衡負荷の場合、一相分の等価回路で計算できる
2. 線間電圧と相電圧の関係(Y結線の場合:線間電圧 = √3 × 相電圧)をしっかり理解する
3. 三相電力の計算:P = 3RI²(抵抗での消費電力に3を掛ける)
4. Δ結線のコンデンサをY結線に変換する方法:C' = 3C
5. 力率改善(力率1にする)には、回路のリアクタンス成分(虚数部)をゼロにする
6. 並列回路の合成インピーダンスの計算:Z = (Z₁·Z₂)/(Z₁+Z₂)
7. 複素数の計算(有理化、実部と虚部の分離)を正確に行う
8. 虚数部をゼロにする条件から方程式を立て、必要なコンデンサ容量を求める
この問題は、三相交流回路の電力計算と力率改善の基本を理解しているかを試す良い問題でした!
解説まとめ
(a)問題の解説
まず、\( e_{\mathrm{a}} \)の実効値 \( E_{\mathrm{a}} \) は次のように求められます。
\[ \begin{aligned} E_{\mathrm{a}} &= \frac{100\sqrt{6}}{\sqrt{2}} \\\\[ 5pt ] &= 100\sqrt{3} \ \mathrm{[V]} \end{aligned} \]
したがって、相電圧の実効値 \( E_{\mathrm{ap}} \) は、
\[ \begin{aligned} E_{\mathrm{ap}} &= \frac{100\sqrt{3}}{\sqrt{3}} \\\\[ 5pt ] &= 100 \ \mathrm{[V]} \end{aligned} \]
となります。
負荷は三相平衡であるため、一相分の等価回路を描くと図2のようになります。
図2より、電流 \( I_{\mathrm{a}} \) は次の通りです。
\[ \begin{aligned} I_{\mathrm{a}} &= \frac{E_{\mathrm{ap}}}{\sqrt{R^{2}+(\omega L)^{2}}} \\\\[ 5pt ] &= \frac{100}{\sqrt{5^2 + (100\pi \times 16 \times 10^{-3})^{2}}} \\\\[ 5pt ] &= 14.108 \ \mathrm{[A]} \end{aligned} \]
したがって、三相電力 \( P \) は以下のように求められます。
\[ \begin{aligned} P &= 3R{I_{\mathrm{a}}}^{2} \\\\[ 5pt ] &= 3 \times 5 \times {14.108}^{2} \\\\[ 5pt ] &\approx 2986 \ \mathrm{[W]} \rightarrow 3 \ \mathrm{[kW]} \end{aligned} \]
解説まとめ
(b)問題の解説
電源の相電圧 \( E_{\mathrm{ap}} \) は、\( E_{\mathrm{a}} \) より30°遅れるので、\( I_{\mathrm{a}} \) は \( E_{\mathrm{ap}} \) と同相になります。
すなわち、\( I_{\mathrm{a}} \) を求め、虚数項がゼロとなる静電容量 \( C \) が解となります。
問題図のコンデンサに対して \( \Delta \)-\( \mathrm{Y} \) 変換を行うと、Y接続での静電容量 \( C' \) は以下の通りです。
\[ \begin{aligned} \frac{1}{\omega C'} &= \frac{1}{3\omega C} \\\\[ 5pt ] C' &= 3C \end{aligned} \]
したがって、一相分の等価回路は図3のようになります。
図3において、抵抗 \( R \)、インダクタンス \( L \)、および \( 3C \) の合成インピーダンス \( Z \) は次のように表されます。
\[ \begin{aligned} Z &= \frac{(R + \mathrm{j} \omega L) \cdot \frac{1}{\mathrm{j} 3\omega C}}{(R + \mathrm{j} \omega L) + \frac{1}{\mathrm{j} 3\omega C}} \\\\[ 5pt ] &= \frac{R + \mathrm{j} \omega L}{1 - 3\omega^2 LC + \mathrm{j} 3\omega RC} \end{aligned} \]
よって、電流 \( I_{\mathrm{a}} \) は次のようになります。
\[ \begin{aligned} I_{\mathrm{a}} &= \frac{E_{\mathrm{ap}}}{Z} \\[10pt] &= E_{\mathrm{ap}} \cdot \frac{1 - 3\omega^2 LC + \mathrm{j} 3\omega RC} {R + \mathrm{j} \omega L} \\[10pt] &= E_{\mathrm{ap}} \cdot \frac{(1 - 3\omega^2 LC + \mathrm{j} 3\omega RC) (R - \mathrm{j} \omega L)} {R^2 + (\omega L)^2} \\[10pt] &= E_{\mathrm{ap}} \cdot \frac{ R(1 - 3\omega^2 LC) + 3\omega^2 RLC + \mathrm{j} \left[ 3\omega R^2 C - \omega L(1 - 3\omega^2 LC) \right] } {R^2 + (\omega L)^2} \end{aligned} \]
上式の虚数部がゼロになればよいため、以下の式が成り立ちます。
この式に各値を代入すると、
\[ \begin{aligned} C &= \frac{16 \times 10^{-3}}{3 \times 5^2 + 3 \times (100\pi)^2 \cdot (16 \times 10^{-3})^2} \\\\[ 5pt ] &\approx \frac{16 \times 10^{-3}}{75 + 75.798} \\\\[ 5pt ] &\approx 0.1061 \times 10^{-3} \rightarrow 1.1 \times 10^{-4} \ \mathrm{[F]} \end{aligned} \]
と求められます。